【AI】人工智能导论汇总
复习汇总
Agent的环境性质:可观测/不可观测、确定的/随机的、已知的/未知的…等等。
-
完全可观察与部分可观察:如果Agent的传感器在每个时间点上都能获取环境的完整状态(或传感器能够检测所有与行动决策相关的信息),则任务环境是完全可观察的,否则构成部分可观察环境。噪声、不精确传感器或传感器丢失部分数据,都可能导致环境成分部分可观察。
-
确定性与随机性环境:如果环境的下一个状态完全取决于当前状态和Agent执行的动作,则该环境是确定的;否则,它是随机的。事实上,如果环境是部分可观察的,则一般可以将其建模为随机性环境。
-
已知和未知:这里指的是Agent的知识状态,比如环境物理法则等。在已知环境中,所有行动的后果是给定的(尽管针对随机环境,其后果呈现出概率特性,但仍然可以看作是已知);如果环境未知,则Agent需要学习环境如何工作,以便做出最好决策。环境的已知与否与可观察性不是一回事,环境已知与否只是对环境的物理规则或知识的刻画,而可观察性是指能否完全对环境状态进行观测获得。
常见的无信息搜索,及其特点。
常见的无信息搜索:广度优先搜索、深度优先搜索、深度受限搜索、迭代加深的深度优先搜索、一致代价搜索(Dijkstra算法)、双向搜索
常见的无信息搜索评价:
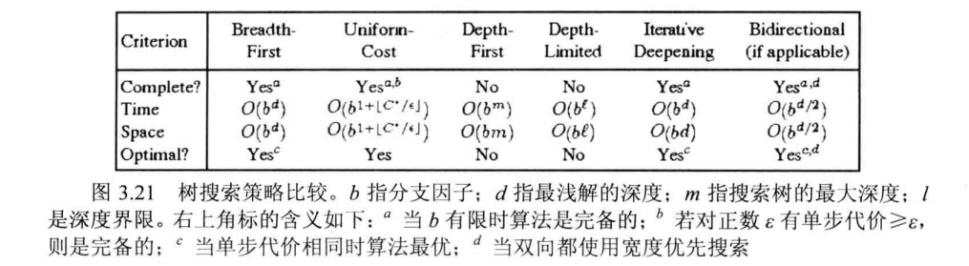
算法的完备性、最优性、时间复杂度、空间复杂度。

一般的树搜索、图搜索。
搜索算法的一般流程:
1 | 1. 初始化 |
Tree-search:
1 | frontier = {A} ①初始化 |
Graph-search:
1 | frontier = {S}, closed = ⌀ ①初始化 |
什么是A*搜索。在A*搜索中,什么是启发函数的可纳性、一致性(单调性)、信息度?
A*算法的空间复杂度很高怎么办?剪枝。


可纳性:估计代价比实际代价低
一致性:三角不等式



根据松弛的方法构造启发式函数h(n):
局部搜索算法。爬山法;模拟退火算法;遗传算法;探索vs.利用。
局部搜索算法的定义:

常见的爬山策略:最陡上升、随机爬山、首选爬山、随机重启

算法只需要记录当前状态和目标函数值,因此空间复杂度为。


模拟退火算法:既考虑“上山”,也考虑“下山”


局部束搜索:可以理解为k倍慢的爬山法

遗传算法:三个主要算子:选择、交叉、变异。





探索&利用
探索:在搜索中将未知知识变成已知
利用:利用知识进行搜索
爬山法:纯利用f(知识),有效率但无完备性
随机:纯搜索,低效但完备
模拟退火:初期探索多,后期利用多
遗传算法的选择、交叉(利用为主,探索为辅)、变异(剧烈探索)
对抗搜索。极小极大搜索、Alpha-beta搜索及剪枝。
博弈树

极大极小算法(深度优先)


Alpha-Beta搜索


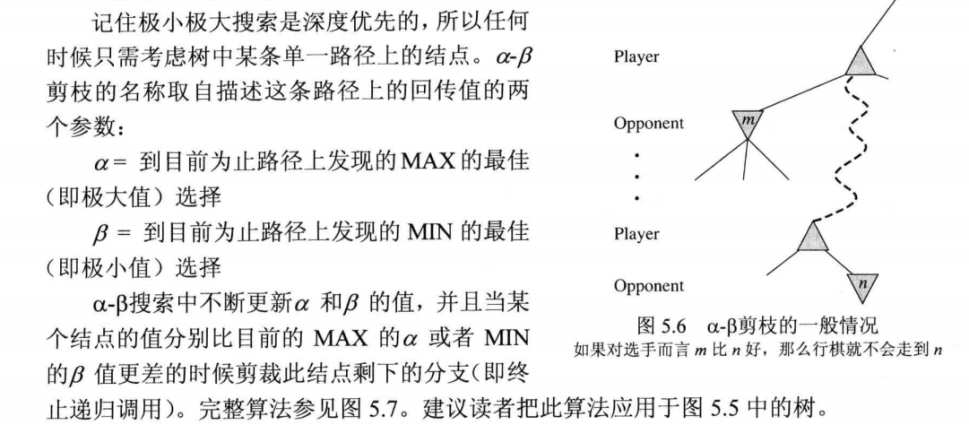

剪枝的本质:在搜索树中忽略那些不影响最后决策的子树。

什么是约束满足搜索?如何将一个实际问题形式化为约束满足问题
什么是约束满足问题:(状态从原子化表示转换为因子化表示)




如何将一个实际问题形式化为约束满足问题:说清楚X、Domain、Constrain三者都是什么。
什么是弧相容?弧相容检查的时间复杂度?
弧相容(arc consistency):变量值域中的所有取值满足该变量的所有二元约束,与两个变量有关(如SA≠NSW)
AC-3算法时间复杂性:CSP有n个变量,每个变量的域大小不超过d,带有c个二元约束,算法的时间复杂度为。

- Arc-3弧相容检查算法

目前有一个问题样例,有三个变量A、B、C,每个变量的值域为{0,1,2,3,4},约束为A=B+1和B=2C,请用AC-3算法进行求解并说明完整的求解流程。
你好,这是Bing。我可以帮你解答这个问题。😊
AC-3算法是一种用于求解约束满足问题(CSP)的弧相容算法,它可以消除变量域中不满足二元约束的值,从而缩小搜索空间¹²。AC-3算法的基本思想是维护一个弧相容队列,其中存放了CSP中的所有弧,每次从队列中取出一条弧(X_i,X_j),并检查X_i是否对X_j弧相容,即X_i的每个值是否有与之相容的X_j的值。如果没有,就删除X_i的这个值,并将所有与X_i有约束的变量和X_i组成的弧重新加入队列。重复这个过程直到队列为空或者某个变量的域为空¹³⁴。
AC-3算法的伪代码如下¹:
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
>inputs: csp, a binary CSP with components (X,D,C)
>local variables: queue, a queue of arcs, initially all the arcs in csp
>while queue is not empty do
>(Xi,Xj) <- REMOVE-FIRST(queue)
>if REVISE(csp,Xi,Xj) then
if size of Di = 0 then return false
for each Xk in Xi NEIGHBORS - {Xj} do
add (Xk,Xi) to queue
>return true
>function REVISE(csp,Xi,Xj) return true if we revise the domain of Xi
>revised <- false
>for each x in Di do
>if no value y in Dj allows (x,y) to satisfy the constraint between Xi and Xj then
delete x from Di
revised <- true
>return revised对于你给出的问题样例,有三个变量A、B、C,每个变量的值域为{0,1,2,3,4},约束为A=B+1和B=2C,我们可以用AC-3算法进行求解,并说明完整的求解流程如下:
- 首先,构造约束图,其中有三个节点A、B、C,分别代表三个变量,有两条有向边(A,B)和(B,C),分别代表两个约束。
- 然后,将所有的弧加入队列,即{(A,B),(B,A),(B,C),(C,B)}。
- 从队列中取出一条弧,假设是(A,B),检查A是否对B弧相容。由于A=B+1,所以当B取0时,A只能取1;当B取1时,A只能取2;当B取2时,A只能取3;当B取3时,A只能取4;当B取4时,A没有可取的值。因此,我们可以删除A的域中的0这个值,并将与A有约束的变量和A组成的弧(B,A)加入队列。此时,队列为{(B,A),(B,C),(C,B),(B,A)},A的域为{1,2,3,4}。
- 从队列中取出一条弧,假设是(B,A),检查B是否对A弧相容。由于A=B+1,所以当A取1时,B只能取0;当A取2时,B只能取1;当A取3时,B只能取2;当A取4时,B只能取3。因此,我们可以删除B的域中的4这个值,并将与B有约束的变量和B组成的弧(C,B)加入队列。此时,队列为{(B,C),(C,B),(B,A),(C,B)},B的域为{0,1,2,3}。
- 从队列中取出一条弧,假设是(B,C),检查B是否对C弧相容。由于B=2C,所以当C取0时,B只能取0;当C取1时,B只能取2;当C取2时,B没有可取的值;当C取3时,B没有可取的值;当C取4时,B没有可取的值。因此,我们可以删除B的域中的1和3这两个值,并将与B有约束的变量和B组成的弧(A,B)和(C,B)加入队列。此时,队列为{(C,B),(B,A),(C,B),(A,B),(C,B)},B的域为{0,2}。
- 从队列中取出一条弧,假设是(C,B),检查C是否对B弧相容。由于B=2C,所以当B取0时,C只能取0;当B取2时,C只能取1。因此,我们可以删除C的域中的2,3,4这三个值,并将与C有约束的变量和C组成的弧(B,C)加入队列。此时,队列为{(B,A),(C,B),(A,B),(C,B),(B,C)},C的域为{0,1}。
- 从队列中取出一条弧,假设是(B,A),检查B是否对A弧相容。由于A=B+1,所以当B取0时,A只能取1;当B取2时,A只能取3。因此,我们可以删除A的域中的2和4这两个值,并将与A有约束的变量和A组成的弧(B,A)加入队列。此时,队列为{(C,B),(A,B),(C,B),(B,C),(B,A)},A的域为{1,3}。
- 从队列中取出一条弧,假设是(C,B),检查C是否对B弧相容。由于B=2C,所以当C取0时,B只能取0;当C取1时,B只能取2。因此,我们不需要删除C的域中的任何值,并且不需要加入任何新的弧到队列中。此时,队列为{(A,B),(C,B),(B,C),(B,A)},C的域为{0,1}。
- 从队列中取出一条弧,假设是(A,B),检查A是否对B弧相容。由于A=B+1,所以当B取0时,A只能取1;当B取2时,A只能取3。因此,我们不需要删除A的域中的任何值,并且不需要加入任何新的弧到队列中。此时,队列为{(C,B),(B,C),(B,A)},A的域为{1,3}。
- 从队列中取出一条弧,假设是(C,B),检查C是否对B弧相容。由于之前已经检查过这条弧,并且没有改变过任何变量的域,所以我们不需要再次检查,并且不需要加入任何新的弧到队列中。此时,队列为{(B,C),(B,A)}。
- 从队列中取出一条弧,假设是(B,C),检查B是否对C弧相容。由于之前已经检查过这条弧,并且没有改变过任何变量的域,所以我们不需要再次检查,并且不需要加入任何新的弧到队列中。此时,队列为{(B,A)}。
- 从队列中取出一条弧,假设是(B,A),检查B是否对A弧相容。由于之前已经检查过这条弧,并且没有改变过任何变量的域,所以我们不需要再次检查,并且不需要加入任何新的弧到队列中。此时,队列为空。
- 因为没有发现任何变量的域为空,并且所有的弧都已经检查
- A={1,3} B={0,2} C={0,1}
- 所以(A,B,C)=(1,0,0)或(3,2,1)
特殊结构上的约束满足搜索。树结构上的约束满足搜索。
回溯法解约束满足搜索问题
变量排序:
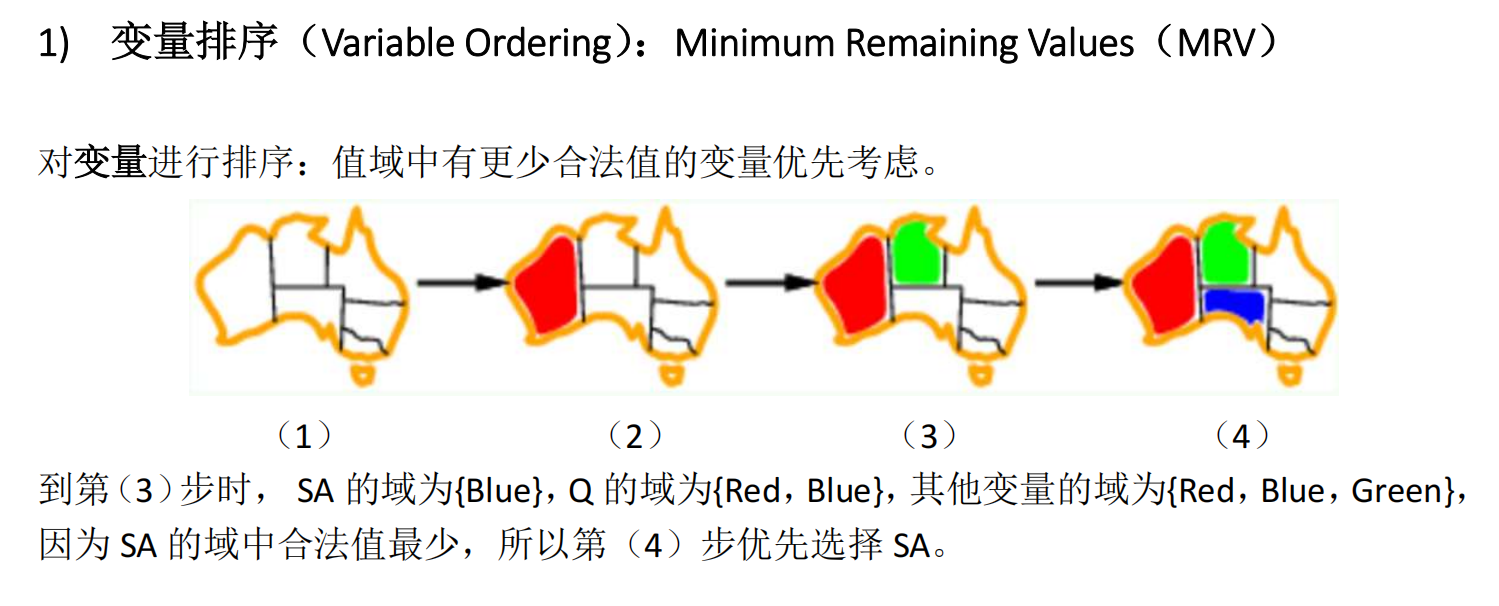
值排序:
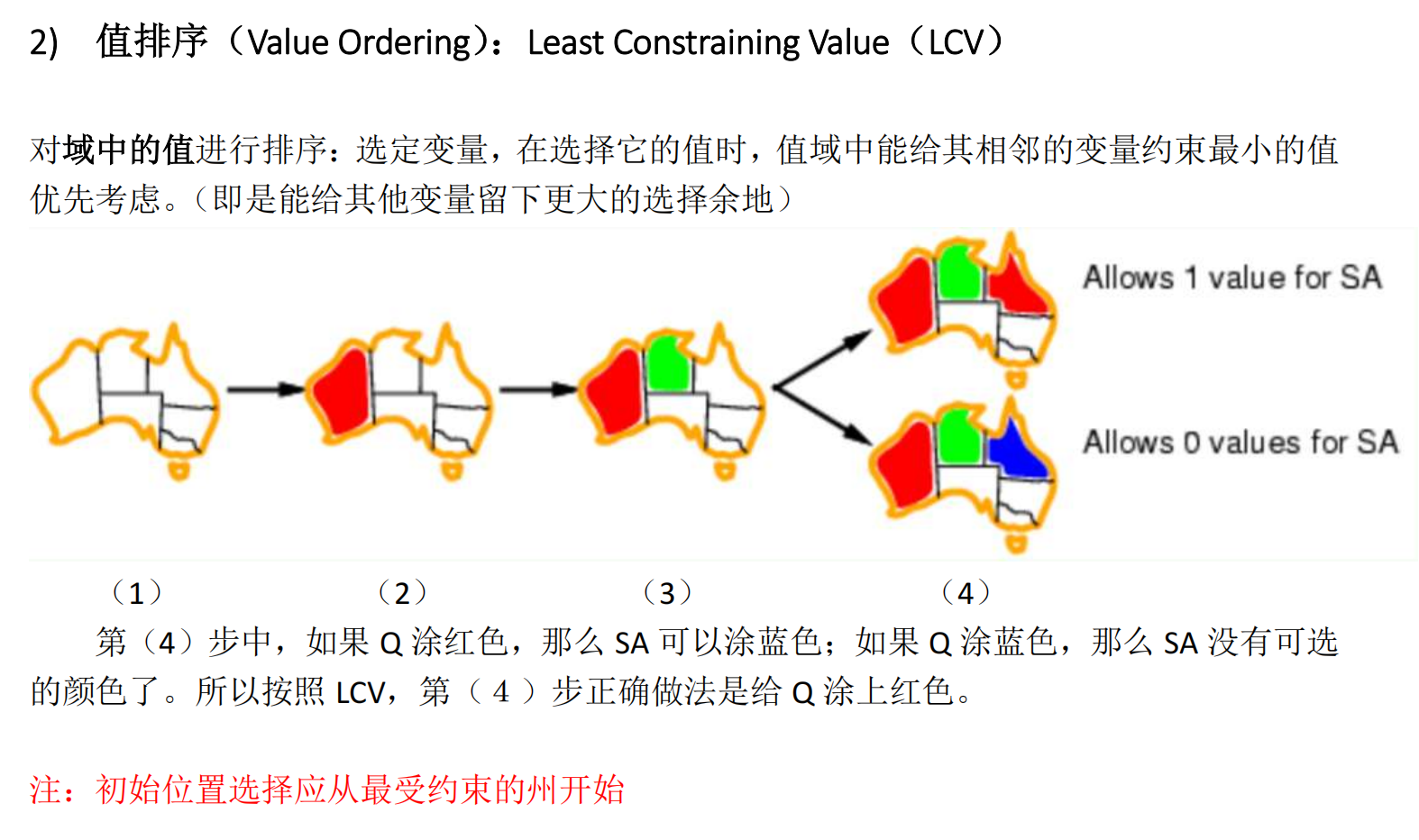
不确定的表示。概率公理、加法公式和乘法公式、条件独立性。概率推理。

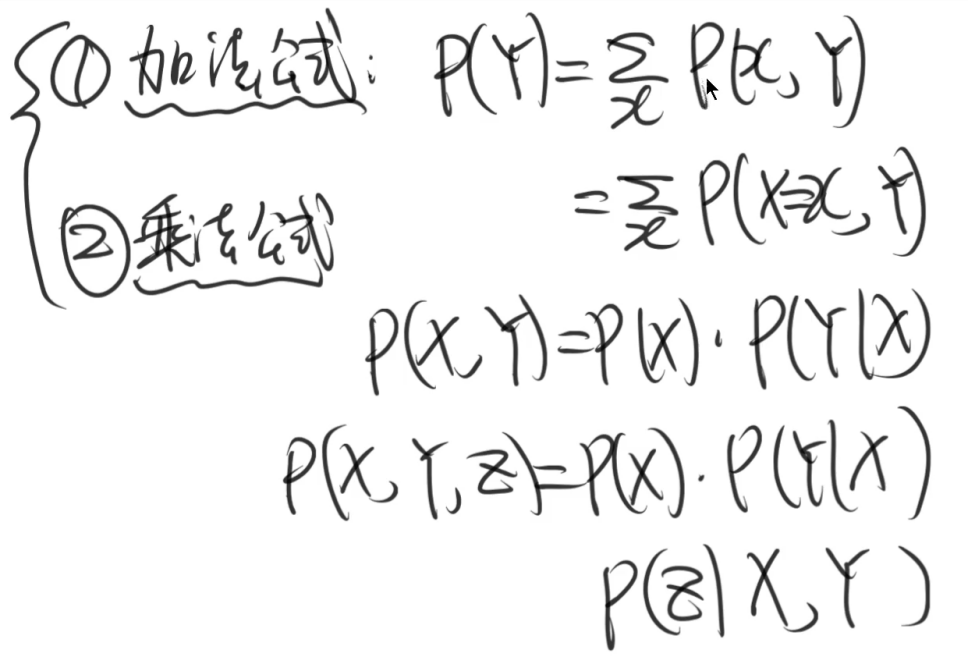
贝叶斯网络。贝叶斯网络的语义;全联合概率分布表示为条件分布之积;马尔可夫覆盖。会将P(X|MB(X))表示为贝叶斯网络中各条件分布的表达式。

贝叶斯网络的语义:
基于对联合概率分布的表示、基于对条件依赖性(条件独立性)的编码
贝叶斯网络中的条件独立性:
- 给定父节点,一个节点条件独立于它的非后代结点
- 给定节点的父节点,子节点以及子节点的父节点(Markov Blanket),这个节点条件独立与网络中的所有其他节点
马尔科夫覆盖MB:
有
精确推理:

贝叶斯网络上的不确定推理:先验采样、拒绝采样、似然加权采样、吉布斯采样。建议参考cs188对应的贝叶斯网络ppt中的各个例题,会对贝叶斯网络进行吉布斯采样。
精确推理的时间复杂度太高,往往是不实际的。因此要通过采样进行近似推理。



马尔可夫决策过程和强化学习。
什么是马尔可夫决策过程(Markov Decision Process)?
马尔可夫决策过程:S, A, T, R, Gamma
解:Pi
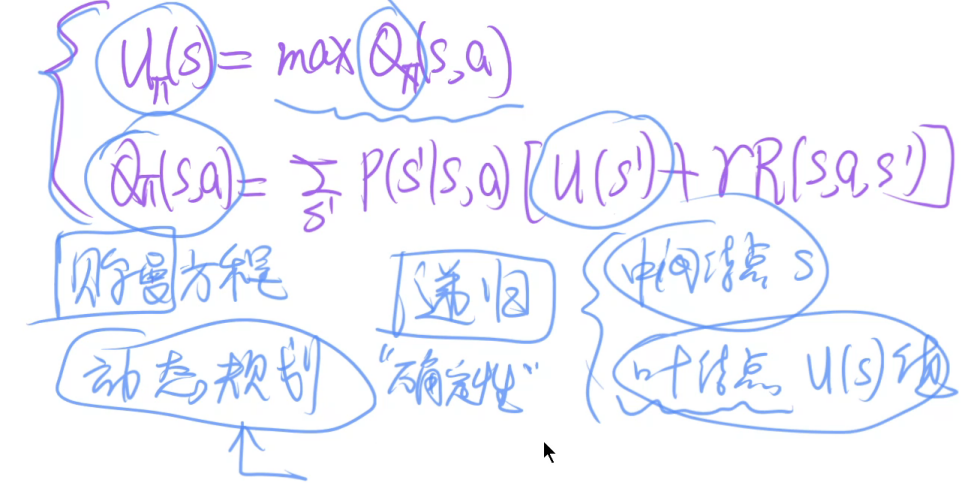
值函数: 、
策略函数:

贝尔曼方程(基本)
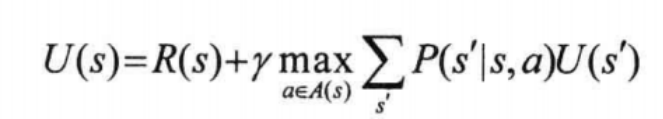
贝尔曼方程(迭代版本)
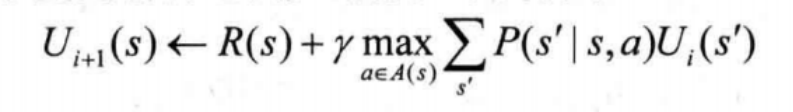
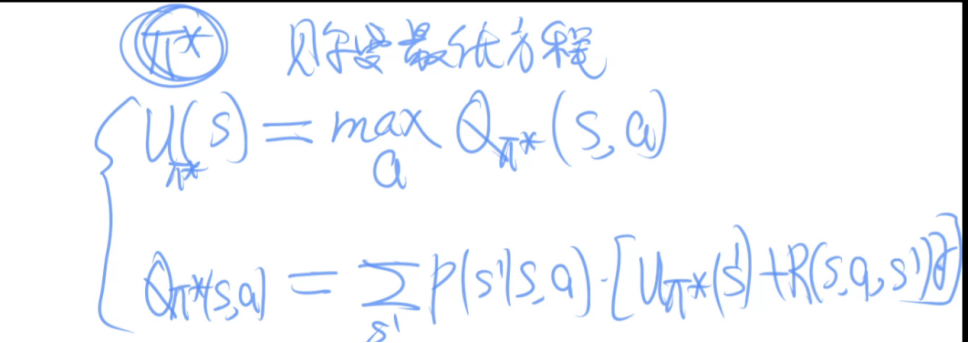
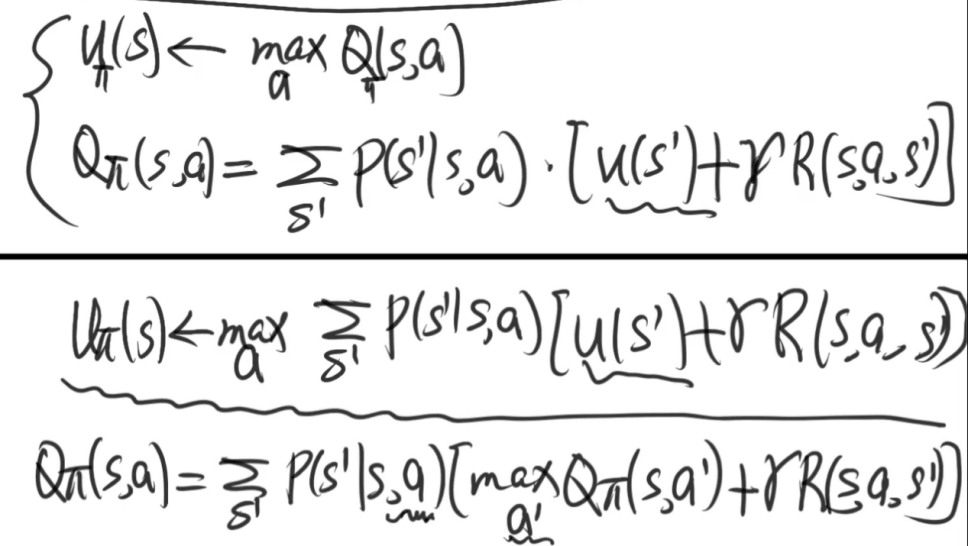

值迭代算法


策略迭代
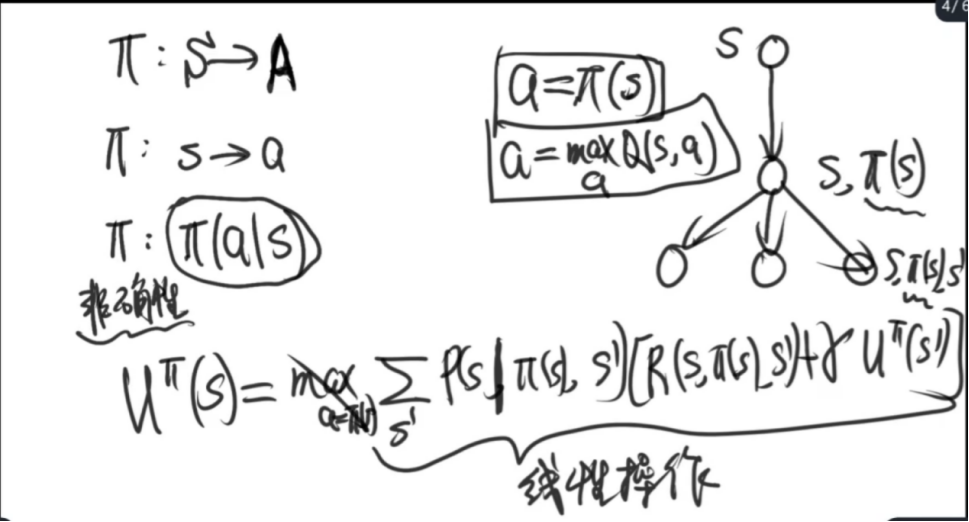
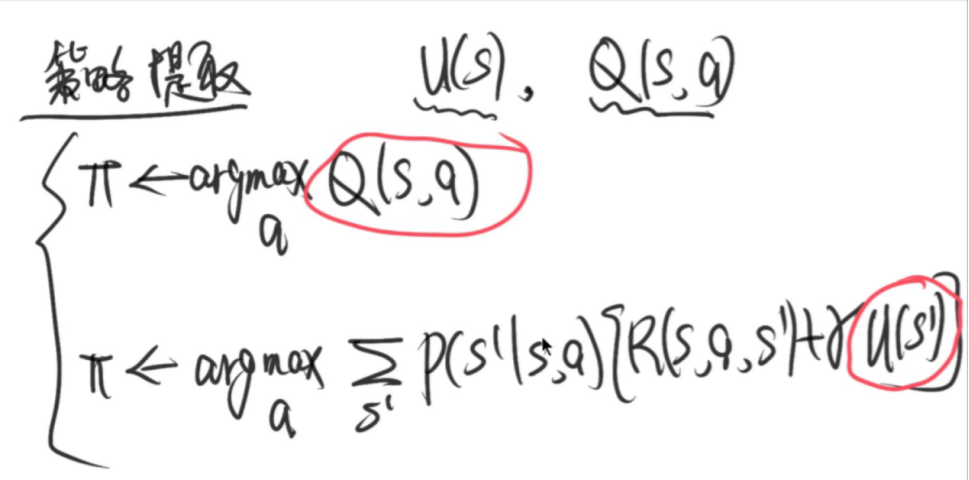

理解主动强化学习/被动强化学习;在线(On-policy,同策略学习)/(Off-policy,异策略)离线学习;基于模型的学习/无模型的学习。掌握基于模型的方法(对模型进行估计)、Q学习、TD学习。建议理解cs188对应的强化学习的ppt中的各种方法和例题。
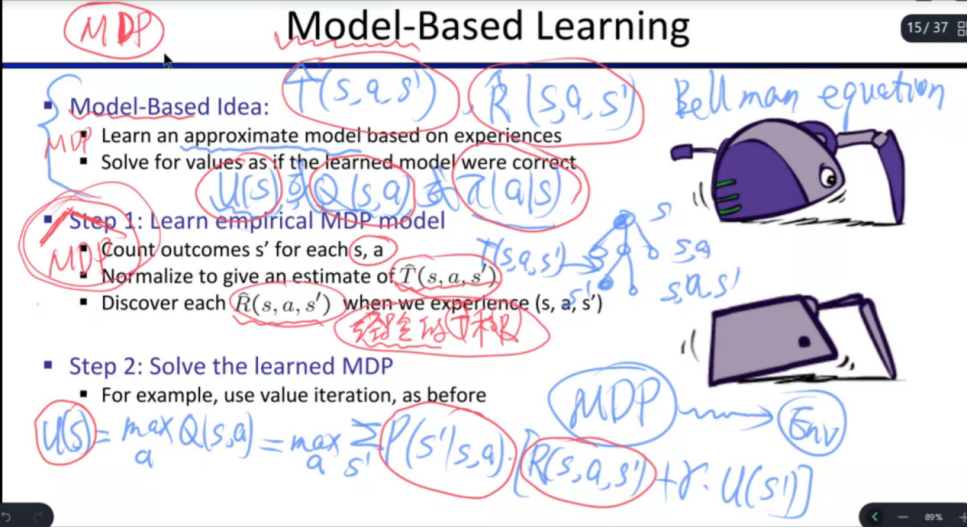
被动强化学习:给定策略
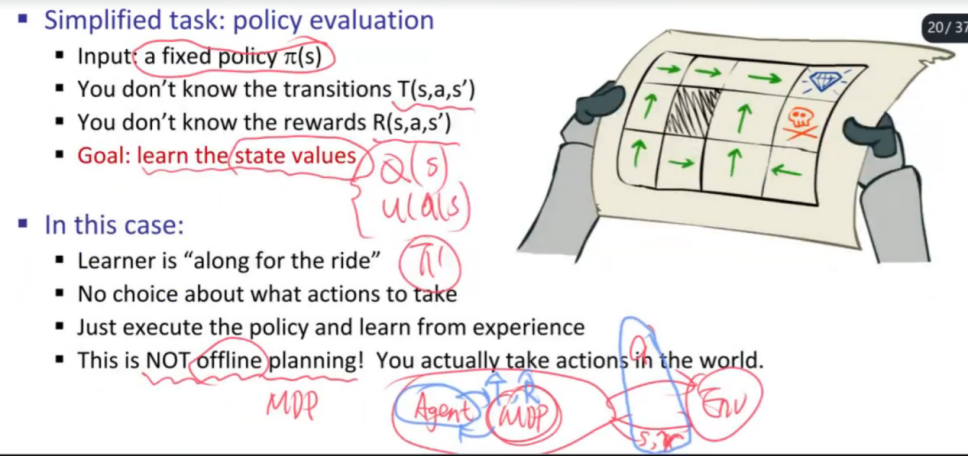

TD学习


主动强化学习



- TD被动强化学习偏向于利用已经给定的策略
- Q主动强化学期既有利用策略,同时不断进行策略提升(探索)以优化策略。
算法实例
- A*搜索:https://www.redblobgames.com/pathfinding/a-star/introduction.html
- 模拟退火搜索:https://zhuanlan.zhihu.com/p/266874840
- 约束满足问题:https://dspace.mit.edu/bitstream/handle/1721.1/36896/5/16-410Fall-2003/NR/rdonlyres/Aeronautics-and-Astronautics/16-410Principles-of-Automated-Reasoning-and-Decision-MakingFall2003/CBCE78FB-85FE-40C0-92ED-0EBB3F56356A/0/l6b_c_p_handout.pdf
- 搜索:https://zhuanlan.zhihu.com/p/65219446
- 隐马尔可夫模型:https://sm1les.com/2019/04/10/hidden-markov-model/






